Study/AI

Doc2Vec , LDA

z 2021. 7. 12. 16:40
728x90

 문장 수준 임베딩

1. Doc2Vec

Word2Vec에 이어 구글 연구 팀이 개발한 문서 임베딩 기법이다.

문장 전체에 대해 단어 k개씩 슬라이딩해가며 단어 k개가 주어졌을 때 다음 단어를 맞추는 과정을 학습한다.

 

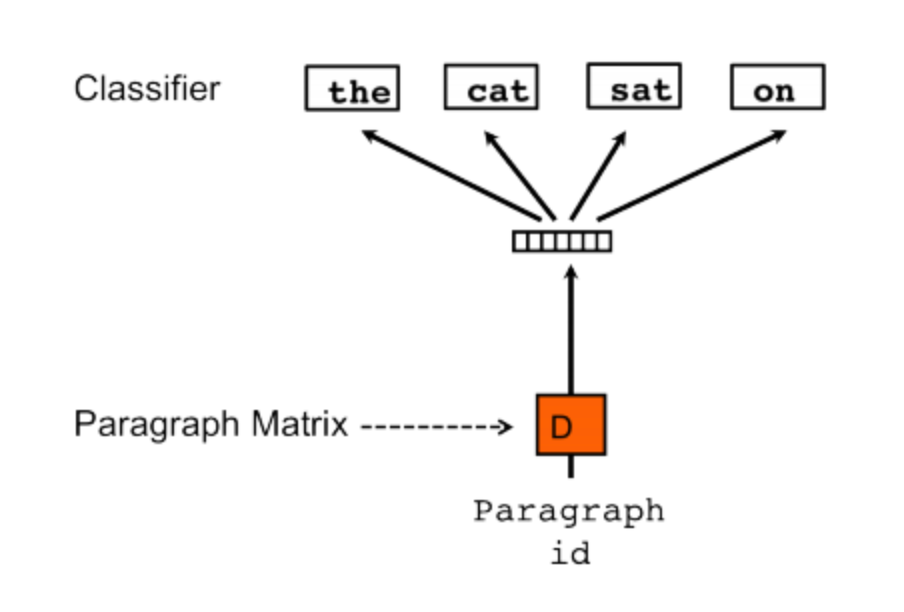
예를 들어, 'The cat sat on the mat'라는 문장에서 k=3일 때 아래 그림처럼 the, cat, sat으로 on을 예측한다.

이 과정을 한 단어씩 sliding하며 문장 내 모든 단어에 대해 예측하는 과정을 학습하는 것이다.

 

 

 

모델 학습 구조)

Doc2Vec 모델은 아래 로그 확률 평균을 최대화하는 과정에서 학습된다.

 

 

이는 학습 데이터 문장 하나의 단어 개수가 T일 때 해당 문장의 로그 확률의 평균이다.

위 수식의 값이 커진다는 것은 모델에 이전 k개 단어들을 입력하면 모델이 다음 단어, target을 잘 맞춘다는 뜻이다.

 

위 수식에서 정의 된 확률을 다음과 같이 계산한다. 

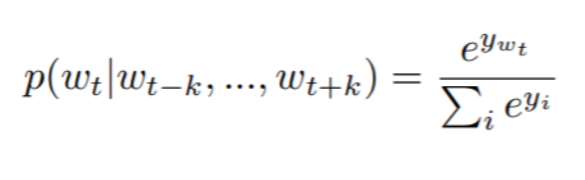
  • w_t : 문장 내 t번째 단어
  • y_i : i번째 단어 점수 (score)
  • h : 벡터 반환 함수 (벡터 시퀀스가 주어졌을 때 평균을 취하거나 이어 붙여 고정된 길이의 벡터 반환)

 

단어 Score인 Y를 만드는 방식은 다음과 같다.

 

이전 k개의 단어들을 W라는 단어 행렬에서 참조한 뒤 평균을 취하거나 이어 붙인다. 여기에 U라는 행렬을 내적하고 바이어스 벡터 b를 더해준다. 이렇게 만든 y에 소프트맥스를 취하면 확률 벡터가 나온다. U의 크기는 어휘 집합 크기 x 임베딩 차원수다.

 

다음 단어를 맞추는 과정에서 문맥 단어들에 해당하는 W 행렬의 벡터들이 업데이트되고, 문장 전체를 한 단어씩 슬라이딩하면서 학습한다.

주변 이웃 단어 집합, 즉 문맥이 유사한 단어 벡터는 벡터 공간에 가깝게 임베딩된다. 학습이 종료되면 W를 각 단어의 임베딩으로 쓴다.

 

 

더 나아가, 위 그림에서 문서 ID를 넣어서 다음 단어를 예측하는 것을 살펴보자.

위 Y 관련 수식에서 계산할 때 D라는 문서행렬에서 해당 문서 ID에 해당하는 벡터를 참조해 h함수에 다르단어 벡터들과 함께 입력하는 것 외에 나머지 과정은 동일하다. 이같은 방식을 PV-DM이라고 이름을 붙였다. 

 

PV-DM

 

학습이 종료되면 문서수 X 임베딩 차원 수 크기를 가지는 문서 행렬 D를 각 문서의 임베딩으로 사용한다. Le & Mikolov는 이렇게 만든 문서 임베딩이 해당 문서의 주제 정보를 함축한다고 설명한다. 이는 문서 임베딩은 동일한 문서 내 존재하는 모든 단어와 함께 학습할 기회를 갖기 때문이다. 또한 저자들은 PV-DM은 단어 등장 순서를 고려하는 방식으로 학습하기 때문에 순서 정보를 무시하는 백오브워즈 기법 대비 강점이 있다고 주장한다.

 

 

지금까지는  Word2Vec의 CBOW 모델과 유사하게, 문맥 단어로 타깃 단어를 예측하는 방식으로 진행되었다. 이와 반대로 Word2Vec의 skip-gram 모델 방식처럼 타깃 단어를 통해 문맥 단어를 예측하는 모델인 PV-DBOW(the Distributed Bag of Words version of Paragraph Vector)을 그림을 통해 살펴보자.

 

PV-DBOW

똑같이 문서 ID를 가지고 문맥 단어를 맞춘다. 따라서 문서 ID에 해당하는 문서 임베딩엔 문서에 등장하는 모든 단어의 의미가 반영된다.

 

2. LDA (잠재 디레클레 할당)

주어진 문서에 대해 각 문서에 어떤 토픽(주제)들이 존재하는지에 대한 확률 모형이다. 

말뭉치 이면에 잠재된 토픽을 추출한다는 의미에서 '토픽 모델링' 이라고 부르기도 한다. 

 

LDA는 말뭉치 이면에 존재하는 정보를 추론하는, 잠재 정보를 알아내는 과정이므로 잠재(Latent)라는 단어가 붙으며,  변수 중 디레클레 분포를 따르는 변수가 있기 때문에 디레클레(Dirichlet)라는 단어로 명명되었다.

 

 

모델 개요)

LDA는 토픽별 단어의 분포, 문서별 토픽의 분포 모두를 추정해낸다.

문서를 토픽 확률 분포로 나타내 각각을 벡터화한다는 점에서 LDA를 임베딩 기법의 일종으로 이해할 수 있다.

 

LDA

 

 

위 그림 우측에 있는 " Topic Proportions, assignments " 가 핵심 프로세스다. 이는 문서의 말뭉치로부터 얻은 주제 분포로부터 주제를 뽑고, 그 주제에 해당하는 단어를 뽑아 문서가 생성되는 과정을 확률 모형으로 모델링한 것이기 때문이다.

 

 

아키텍처)

 

 

LDA는 주제의 단어 분포(Φ)와 문서의 주제 분포(θ)의 결합으로 문서 내 단어들이 생성된다는 가정 하에 만들어진다. 

학습은 실제 관찰이 가능한 말뭉치(문서와 단어)를 가지고 우리가 알고 싶은 토픽의 단어 분포, 문서의 토픽 분포를 추정하는 과정이다.

 

D 문서 총 갯수
K 토픽의 총 갯수
N d번째 문서의 총 단어 갯수
Θ 문서당 토픽 분포, Θd ~ Dir(α) for d∈{1,2,...,D}
Φ 토픽당 단어 분포, Φk ~ Dir(β) for k∈{1,2,...,K}
해당 단어의 토픽 분포, zd,n ~ 
d번째 문서의 n번째 단어, wd,n ~ 

 

유일하게 관찰할 수 있는 변수는 m번째 문서에 등장하는 n번째 단어인 w이며, 우리는 이 정보만을 가지고 사용자가 지정하는 하이퍼파라미터인 α,  β 를 제외한 모든 잠재 변수를 추정해야 한다.

w에 영향을 주는 변수는 w의 주제를 나타내는 변수 z와 k번째 주제에 대한 단어 확률 분포를 나타내는 변수 Φ이다. m번째 문서의 n번째 단어 주제를 나타내는 변수 z는 m번째 문서에 대한 주제 확률 분포를 나타내는 변수 θ에 영향을 받으며, 이 변수는 디레클레 분포 변수 α에 영향을 받아 디레클레 분포를 따른다. 마찬가지로, k번째 주제에 대한 단어 확률 분포를 나타내는 변수 Φ는 디레클레 분포 변수 β에 영향을 받아 디레클레 분포를 따른다.

 

🌱  디리클레 분포란?
:  K차원 벡터 요소 모두 양수이며, 모두 더한 값이 1인 경우 확률 값이 정의되는 연속확률분포로 
   베이즈 확률에서 사전 확률로 많이 사용된다.

Dirichlet Distribution

 

깁스 샘플링 (Gibbs Sampling) 을 이용한 단어 생성 과정)

🌱   깁스 샘플링이란?

: 하나의 변수만 랜덤변수로 놓고 나머지는 고정시킨 채 표본을 뽑는 기법이다.

위에서 언급했던 LDA가 가정하는 문서 생성 과정이 합리적이라고 하면, 해당 확률 모델이 우리가 갖고 있는 말뭉치를 제대로 설명할 수 있을 것이다. 즉, 토픽의 단어 분포와 문서의 토픽 분포의 결합 확률이 커지도록 해야한다.

LDA에 깁스 샘플링을 적용하여 우리가 구할 수 있는 값은 다음과 같다. 식 전체는 w와 z−i가 주어졌을 때 문서의 번째 단어의 토픽이 j일 확률을 뜻하고, z−i는 i번째 단어의 토픽 정보를 제외한 모든 단어의 토픽 정보를 가리킨다. 

 

 

  1. 초기에 모든 단어에 특정 토픽을 할당한다.
  2. 첫 번째 문서 첫 번째 단어 z0,0의 토픽 정보를 지운다.
  3. 해당 단어를 제외하고 토픽이 할당된 z−i와 위 전체 식을 이용하여 z0,0에 가장 적합한 토픽을 찾아 새로 할당한다.
  4. 현재 문서에서 차례대로 다음 단어, 이후 다음 문서, … 이런 식으로 반복하며 2, 3 과정을 반복한다.
  5. 충분히 반복하다 보면 수렴하게 된다.

 

위 과정을 거쳤을 때 나타난 결과 식

 

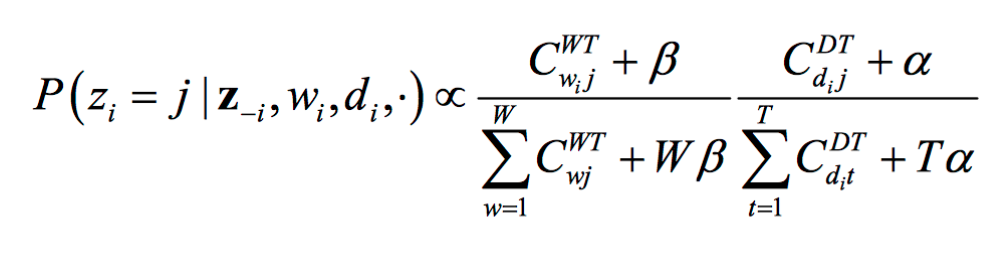
위 식은 번째 문서의 번째 단어 의 토픽이 일 확률은 다음의 두 가지에 영향을 받는다는 것을 뜻한다.

  • 토픽 에 할당된 전체 단어 중에서 해당 단어의 점유율이 높을수록 일 확률이 크다.
  • 가 속한 문서 내 다른 단어가 토픽 에 많이 할당되었을수록 일 확률이 크다.

 

from gensim import corpora
from preprocess import get_tokenizer
from gensim.models import ldamulticore

docs, tokenized_corpus = [],[]
tokenizer = get_tokenizer("mecab")

with open('doc.txt', 'r') as f:
    for doc in f:
        tokens = list(set(tokenizer.morphs(doc.strip())))
        docs.append(doc)
        tokenized_corpus.append(tokens)
        
dictionary = corpora.Dictionary(tokenized_corpus)
corpus = [dictionary.doc2bow(text) for text in tokenized_corpus]

LDA = ldamulticore.LdaMulticore(corpus, id2word=dictionary, num_topics=30, workers=4)
all_topics = LDA.get_document_topics(corpus, minimum_probability=0.5, per_word_topics=False)

for idx, topic in enumerate(all_topics):
    	print(idx, topic)

 

 

728x90
저작자표시 비영리 변경금지